Version 0.2 for commenting
A free account on hypothes.is is required to leave comments.
To leave a comment, select text → Annotate. All comments are public.

3  Simple AgroClimate Metrics

Parker et al. (2022) identify a dozen agroclimate metrics derived 100% from weather data and provide physiologically relevant information for growers. This chapter provides R code to compute most of these agroclimate metrics using historic observed data from Cal-Adapt.

3.1 Load Packages

As usual, we start by loading a bunch of packages into memory and specifying our preferences for conflicting function names:

library(caladaptr)
library(units)
library(ggplot2)
library(dplyr)
library(tidyr)
library(lubridate)
library(sf)

Set conflicted preferences:

library(conflicted)
conflict_prefer("filter", "dplyr", quiet = TRUE)
conflict_prefer("count", "dplyr", quiet = TRUE)
conflict_prefer("select", "dplyr", quiet = TRUE)

3.2 Fetch Some Data

To compute agroclimate metrics, we’ll first get 20 years of observed data from the gridMet dataset for a location in Colusa County in the Sacramento Valley.

colusa_cap <- ca_loc_pt(coords = c(-122.159304, 39.289291)) %>%
  ca_slug(c("tmmn_day_gridmet", "tmmx_day_gridmet")) %>%
  ca_years(start = 2000, end = 2020) 

colusa_cap

Cal-Adapt API Request
Location(s): 
  x: -122.159
  y: 39.289
Slug(s): tmmn_day_gridmet, tmmx_day_gridmet
Dates: 2000-01-01 to 2020-12-31
 

colusa_cap %>% ca_preflight()

General issues
 - none found
Issues for querying values
 - none found
Issues for downloading rasters
 - none found

plot(colusa_cap)

Next we fetch the data. While we’re at it, we’ll add columns for the climate variable (based on the slug), year, and temperature in Fahrenheit:

colusa_tbl <- colusa_cap %>% 
  ca_getvals_tbl() %>% 
  mutate(dt = as.Date(dt),
         year = year(as.Date(dt)),
         cvar = substr(slug, 1, 4),
         temp_f = units::set_units(val, degF)) %>% 
  select(year, dt, cvar, temp_f)

glimpse(colusa_tbl)

Rows: 15,342
Columns: 4
$ year   <dbl> 2000, 2000, 2000, 2000, 2000, 2000, 2000, 2000, 2000, 2000, 200…
$ dt     <date> 2000-01-01, 2000-01-02, 2000-01-03, 2000-01-04, 2000-01-05, 20…
$ cvar   <chr> "tmmn", "tmmn", "tmmn", "tmmn", "tmmn", "tmmn", "tmmn", "tmmn",…
$ temp_f [degF] 32.45 [degF], 30.11 [degF], 32.09 [degF], 39.11 [degF], 32.27 …

3.3 Growing Degree Days

Growing Degree Days (GDD) are a measure of accumulated heat starting from a specific date / event. You may wonder - what’s the point of tracking accumulated heat, given that it cools down every night? The answer is because many plants seem to keep track of accumulated heat units. Research has shown that many phenological events, like the emergence of fruit, are strongly correlated with accumulated heat, also known as thermal time. Insect phenology is likewise strongly correlated with heat units.

There are a few ways of computing GDD. Parker et al. (2022) recommend the simple average method with a base temperature of 10 °C:

\(GDD = (temp_{max} - temp_{min}) / 2 - temp_{base}\)

Negative GDD values are not biologically meaningful (i.e., plant development generally doesn’t go backwards), so negative GDD values are generally converted to 0 (i.e., Method 1 described by McMaster and Wilhelm (1997)).

Computing daily GDD is fairly straight-forward. We just have to remember to zero-out negative GDD values:

(tbase_c <- set_units(10, degC))                           ## base temp

10 [°C]

colusa_gdd_tbl <- colusa_tbl %>% 
  mutate(temp_c = set_units(temp_f, degC)) %>%             ## create a degC column
  pivot_wider(id_cols = c(year, dt),                       ## make min and max temps separate colums
              names_from = cvar, 
              values_from = temp_c) %>% 
  mutate(gdd = as.numeric(((tmmx+tmmn)/2) - tbase_c)) %>%  ## compute gdd as a numeric value
  mutate(gdd = if_else(gdd < 0, 0, gdd))                   ## zero-out negative values

colusa_gdd_tbl %>% head()

Applying GDD to predict crop development requires 1) a start date (also known as a biofix date), and 2) a crop phenology table. These are not shown here, but are not hard to apply (for an example see the Pistachio Nut Development Decision Support tool).

3.4 Chill Accumulation

Chill accumulation is similar to growing degree days, but for cold. In other words, there are a few phenological events that appear to be strongly correlated with the accumulated amount of chill. An example of this is flowering for many tree crops. Apparently, the trees keep an internal ledger of how cold its been during the winter, and for how long. They use this internal record use to decide when it’s time to come out of their winter dormancy and start flowering. This mechanism probably evolved to help them avoid frost damage.

Researchers have looked at a number of ways to measure accumulated chill, and the one that does the best job at predicting phenology events is called Chill Portions (CP) (Luedeling and Brown 2011). The calculations are a bit complicated, but fortunately there’s a R-package that will compute chill portions. For more info, see here.

3.5 Frost Days

Frost Days (FD) are the number of days per year with minimum temperatures (Tn) ≤ 0 °C (Parker et al. 2022). They can be computed with:

colusa_fd_tbl <- colusa_tbl %>% 
  filter(cvar == "tmmn", temp_f <= set_units(0, degC)) %>% 
  group_by(year) %>% 
  summarise(fd = n())

colusa_fd_tbl

3.6 Last Spring and First Fall Freeze

The Last Spring Freeze (LSF) is defined as the last day of the calendar year prior to 30 June with a Tn ≤ 0 °C. Conversely the First Fall Freeze (FFF) is defined as the first day of the calendar year commencing 1 July with Tn ≤ 0 °C (Parker et al. 2022).

We can find the last freeze date by chaining together dplyr expressions that i) keep only ‘freeze days’ from January through June, ii) group the freeze days by year, and iii) taking the max date for each group:

colusa_lf_tbl <- colusa_tbl %>% 
  filter(cvar == "tmmn", month(dt) <= 6, temp_f <= set_units(32, degF)) %>% 
  group_by(year) %>% 
  summarise(lf = max(dt))

colusa_lf_tbl

Similarly, we can find the first fall freeze by keeping only dates from July - December where the temperature dipped below freezing, then taking the minimum date for each year:

colusa_fff_tbl <- colusa_tbl %>% 
  filter(cvar == "tmmn", month(dt) >= 7, temp_f <= set_units(32, degF)) %>%
  group_by(year) %>% 
  summarise(fff = min(dt))

colusa_fff_tbl

3.7 Freeze-Free Season

The Freeze-Free Season (FFS) is calculated as the difference between the LSF and FFF (FFF [minus] LSF) (Parker et al. 2022). Since we already calculated LSF and FFF, computing the Freeze-Free Season can be done with a simple table join:

colusa_lf_fff_tbl <- colusa_lf_tbl %>% left_join(colusa_fff_tbl, by = "year")
colusa_lf_fff_tbl %>% head()

colusa_lf_fff_ffs_tbl <- colusa_lf_fff_tbl %>% mutate(ffs = fff - lf)
colusa_lf_fff_ffs_tbl

3.8 Tropical Nights and Hot Days

Tropical Nights (TRN) are calculated as the number of nights per year with Tn > 20 °C (68 °F) (Parker et al. 2022). This can be computed with:

colusa_tn_tbl <- colusa_tbl %>% 
  filter(cvar == "tmmn", temp_f > set_units(20, degC)) %>% 
  group_by(year) %>% 
  summarise(tn = n())

colusa_tn_tbl

Hot Days (HD) are defined as when Tx > 38 °C (Parker et al. 2022). The number of hot days per year can be computed with:

colusa_hd_tbl <- colusa_tbl %>% 
  filter(cvar == "tmmx", temp_f > set_units(38, degC)) %>% 
  group_by(year) %>% 
  summarise(hd = n())

colusa_hd_tbl

3.9 Extreme Heat Days

Extreme Heat Days (EHD) are the number of days per year with Tx >98th percentile of summer (June-August) Tx for the 1981–2010 period (Parker et al. 2022). This is similar to HD, but with a threshold value based on the historic record. We can compute the 98th percentile of daily summertime highs with:

colusa_ehd_thresh <- ca_loc_pt(coords = c(-122.159304, 39.289291)) %>%
  ca_slug("tmmx_day_gridmet") %>%
  ca_years(start = 1981, end = 2010) %>% 
  ca_getvals_tbl(quiet = TRUE) %>% 
  filter(month(as.Date(dt)) %in% c(6,7,8)) %>% 
  pull(val) %>% 
  quantile(0.98) %>% 
  set_units(degF)

colusa_ehd_thresh

106.2176 [degF]

Once we have that threshold, we can compute Extreme Heat Days with:

colusa_ehd_tbl <- colusa_tbl %>% 
  filter(cvar == "tmmx", temp_f > colusa_ehd_thresh) %>% 
  group_by(year) %>% 
  summarise(hd = n())

colusa_ehd_tbl

3.10 Heatwaves

Heatwave events (HW) are defined as 3+ consecutive days with Tx > 98th percentile of 1981–2010 summer Tx (as in EHD) (Parker et al. 2022). Using the technique described in [Chapter 4 - Counting Consecutive Events][Counting Consecutive Events], we can compute the number of heatwaves per year.

1. Add a column for extreme heat day, then create a grouped tibble (by year):

colusa_grpd_tbl <- colusa_tbl %>% 
  filter(cvar == "tmmx") %>% 
  mutate(ehd = temp_f > colusa_ehd_thresh) %>%
  group_by(year) %>% 
  arrange(dt)

glimpse(colusa_grpd_tbl)

Rows: 7,671
Columns: 5
Groups: year [21]
$ year   <dbl> 2000, 2000, 2000, 2000, 2000, 2000, 2000, 2000, 2000, 2000, 200…
$ dt     <date> 2000-01-01, 2000-01-02, 2000-01-03, 2000-01-04, 2000-01-05, 20…
$ cvar   <chr> "tmmx", "tmmx", "tmmx", "tmmx", "tmmx", "tmmx", "tmmx", "tmmx",…
$ temp_f [degF] 54.95 [degF], 53.87 [degF], 57.65 [degF], 49.37 [degF], 57.47 …
$ ehd    <lgl> FALSE, FALSE, FALSE, FALSE, FALSE, FALSE, FALSE, FALSE, FALSE, …

2. Create a function that we can pass to group_modify(), will return the number of heatwaves per group (year):

num_hw <- function(data_tbl, key_tbl, num_days = 3) {
  rle_lst <- rle(data_tbl$ehd)
  tibble(num_hw = sum(rle_lst$values & rle_lst$lengths >= num_days))
}

 

3. Apply the heatwave function to the grouped tibble:

colusa_hw_tbl <- colusa_grpd_tbl %>% 
  group_modify(.f = num_hw, num_days = 3)

colusa_hw_tbl

3.11 Diurnal Temperature Range

Diurnal Temperature Range (DTR) is the difference between daily Tx and Tn (Parker et al. 2022). Below we calculate DTR over 1 March to 1 November.

colusa_dtr_tbl <- colusa_tbl %>% 
  filter(month(dt) %in% 3:10) %>% 
  pivot_wider(id_cols = c(year, dt), names_from = cvar, values_from = temp_f) %>% 
  mutate(dtr = tmmx - tmmn)

head(colusa_dtr_tbl)

ggplot(colusa_dtr_tbl %>% mutate(year = as.factor(year)), aes(x=year, y = dtr)) + 
  geom_boxplot() + 
  labs(title = "Diurnal Temperature Range, 2000-2020",
       subtitle = "Colusa, CA", 
       caption = "Dataset: gridMet. Temporal period: March - October",
       x = "", y = "daily temperature range")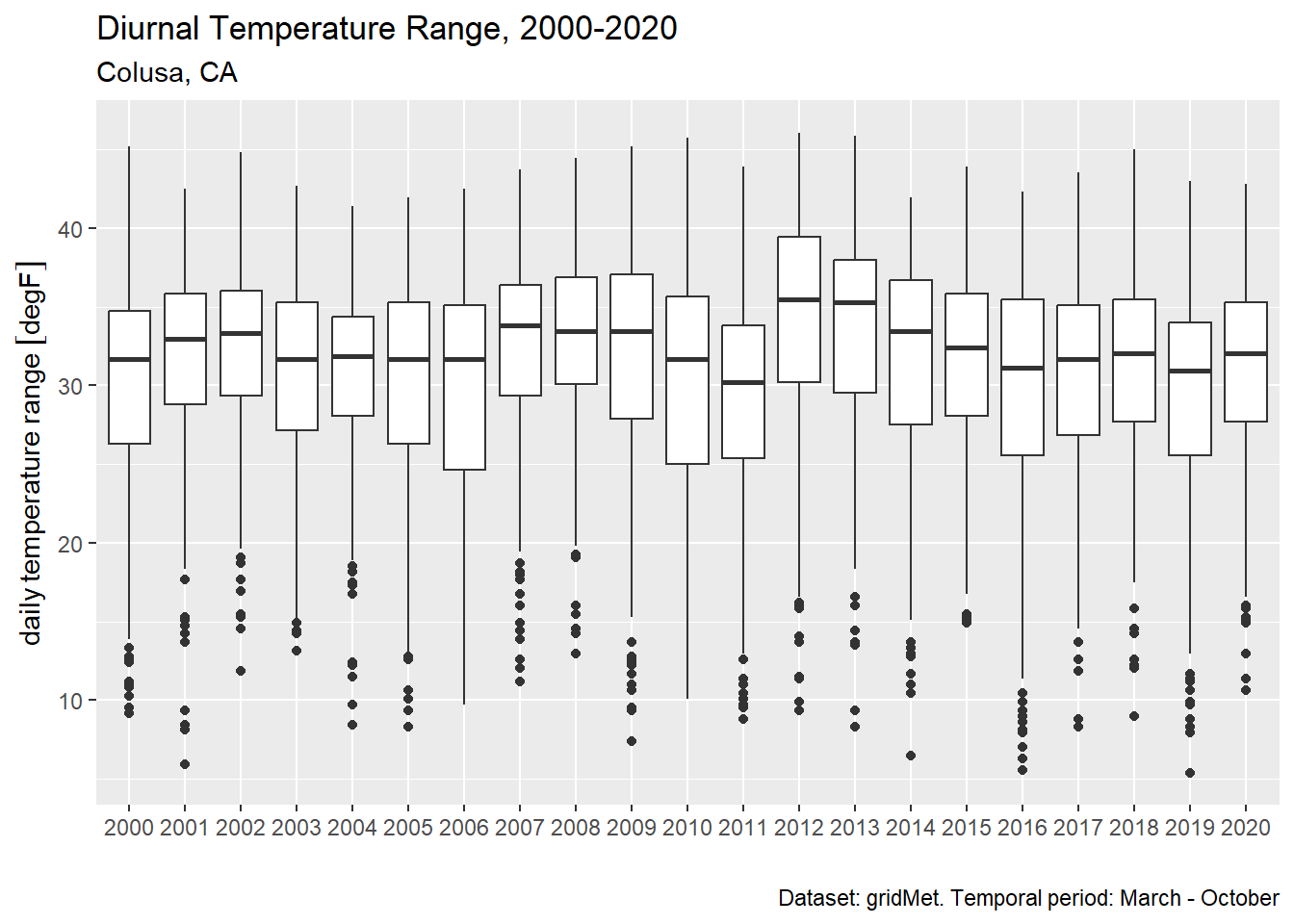

3.12 Reference Evapotranspiration

ETo is calculated following the FAO Penman–Monteith method (Allen and United Nations 1998). We calculate summer (June-August) average ETo for each year 1981–2020 for our analysis. ETo units are mm (Parker et al. 2022).

More coming soon…

Allen, R. G., and Food and Agriculture Organization of the United Nations, eds. 1998. Crop Evapotranspiration: Guidelines for Computing Crop Water Requirements. FAO Irrigation and Drainage Paper 56. Rome: Food; Agriculture Organization of the United Nations.

Luedeling, Eike, and Patrick H. Brown. 2011. “A Global Analysis of the Comparability of Winter Chill Models for Fruit and Nut Trees.” International Journal of Biometeorology 55 (3): 411–21. https://doi.org/10.1007/s00484-010-0352-y.

McMaster, G, and W Wilhelm. 1997. “Growing Degree-Days: One Equation, Two Interpretations.” Agricultural and Forest Meteorology 87 (4): 291–300. https://doi.org/10.1016/S0168-1923(97)00027-0.

Parker, Lauren E., Ning Zhang, John T. Abatzoglou, Steven M. Ostoja, and Tapan B. Pathak. 2022. “Observed Changes in Agroclimate Metrics Relevant for Specialty Crop Production in California.” Agronomy 12 (1): 205. https://doi.org/10.3390/agronomy12010205.