Chapter 5 AgroClimate Metrics
Parker et al. (2022) identify a dozen agroclimate metrics derived 100% from weather data and provide physiologically relevant information for growers. This chapter provides R code to compute most of these agroclimate metrics using historic observed data from Cal-Adapt.
5.1 Load Packages
As usual, we start by loading a bunch of packages into memory and specifying our preferences for conflicting function names:
library(caladaptr)
library(units)
library(ggplot2)
library(dplyr)
library(tidyr)
library(lubridate)
library(sf)Set conflicted preferences:
library(conflicted)
conflict_prefer("filter", "dplyr", quiet = TRUE)
conflict_prefer("count", "dplyr", quiet = TRUE)
conflict_prefer("select", "dplyr", quiet = TRUE)5.2 Fetch Some Data
To compute agroclimate metrics, we’ll first get 20 years of observed data from the gridMet dataset for a location in Colusa County in the Sacramento Valley.
colusa_cap <- ca_loc_pt(coords = c(-122.159304, 39.289291)) %>%
ca_slug(c("tmmn_day_gridmet", "tmmx_day_gridmet")) %>%
ca_years(start = 2000, end = 2020)
colusa_cap## Cal-Adapt API Request
## Location(s):
## x: -122.159
## y: 39.289
## Slug(s): tmmn_day_gridmet, tmmx_day_gridmet
## Dates: 2000-01-01 to 2020-12-31
## colusa_cap %>% ca_preflight()## General issues
## - none found
## Issues for querying values
## - none found
## Issues for downloading rasters
## - none foundplot(colusa_cap)
Next we fetch the data. While we’re at it, we’ll add columns for the climate variable (based on the slug), year, and temperature in Fahrenheit:
colusa_tbl <- colusa_cap %>%
ca_getvals_tbl() %>%
mutate(dt = as.Date(dt),
year = year(as.Date(dt)),
cvar = substr(slug, 1, 4),
temp_f = units::set_units(val, degF)) %>%
select(year, dt, cvar, temp_f)
glimpse(colusa_tbl)## Rows: 15,342
## Columns: 4
## $ year <dbl> 2000, 2000, 2000, 2000, 2000, 2000, 2000, 2000, 2000, 2000, 200~
## $ dt <date> 2000-01-01, 2000-01-02, 2000-01-03, 2000-01-04, 2000-01-05, 20~
## $ cvar <chr> "tmmn", "tmmn", "tmmn", "tmmn", "tmmn", "tmmn", "tmmn", "tmmn",~
## $ temp_f [degF] 32.45 [degF], 30.11 [degF], 32.09 [degF], 39.11 [degF], 32.27 ~5.3 Growing Degree Days
Growing Degree Days (GDD) are a measure of accumulated heat starting from a specific date / event. You may wonder - what’s the point of tracking accumulated heat, given that it cools down every night? The answer is because many plants seem to keep track of accumulated heat units. Research has shown that many phenological events, like the emergence of fruit, are strongly correlated with accumulated heat, also known as thermal time. Insect phenology is likewise strongly correlated with heat units.
There are a few ways of computing GDD. Parker et al. (2022) recommend the simple average method with a base temperature of 10 °C:
Negative GDD values are not biologically meaningful (i.e., plant development generally doesn’t go backwards), so negative GDD values are generally converted to 0 (i.e., Method 1 described by McMaster and Wilhelm (1997)).
Computing daily GDD is fairly straight-forward. We just have to remember to zero-out negative GDD values:
(tbase_c <- set_units(10, degC)) ## base temp## 10 [°C]colusa_gdd_tbl <- colusa_tbl %>%
mutate(temp_c = set_units(temp_f, degC)) %>% ## create a degC column
pivot_wider(id_cols = c(year, dt), ## make min and max temps separate colums
names_from = cvar,
values_from = temp_c) %>%
mutate(gdd = as.numeric(((tmmx+tmmn)/2) - tbase_c)) %>% ## compute gdd as a numeric value
mutate(gdd = if_else(gdd < 0, 0, gdd)) ## zero-out negative values
colusa_gdd_tbl %>% head()## # A tibble: 6 x 5
## year dt tmmn tmmx gdd
## <dbl> <date> [°C] [°C] <dbl>
## 1 2000 2000-01-01 0.250 12.7 0
## 2 2000 2000-01-02 -1.05 12.2 0
## 3 2000 2000-01-03 0.0500 14.2 0
## 4 2000 2000-01-04 3.95 9.65 0
## 5 2000 2000-01-05 0.150 14.2 0
## 6 2000 2000-01-06 -1.35 12.6 0
Applying GDD to predict crop development requires 1) a start date (also known as a biofix date), and 2) a crop phenology table. These are not shown here, but are not hard to apply (for an example see the Pistachio Nut Development Decision Support tool).
5.4 Chill Accumulation
Chill accumulation is similar to growing degree days, but for cold. In other words, there are a few phenological events that appear to be strongly correlated with the accumulated amount of chill. An example of this is flowering for many tree crops. Apparently, the trees keep an internal ledger of how cold its been during the winter, and for how long. They use this internal record use to decide when it’s time to come out of their winter dormancy and start flowering. This mechanism probably evolved to help them avoid frost damage.
Researchers have looked at a number of ways to measure accumulated chill, and the one that does the best job at predicting phenology events is called Chill Portions (CP) (Luedeling and Brown 2011). The calculations are a bit complicated, but fortunately there’s a R-package that will compute chill portions. For more info, see here.
5.5 Frost Days
Frost Days (FD) are the number of days per year with minimum temperatures (Tn) ≤ 0 °C (Parker et al. 2022). They can be computed with:
colusa_fd_tbl <- colusa_tbl %>%
filter(cvar == "tmmn", temp_f <= set_units(0, degC)) %>%
group_by(year) %>%
summarise(fd = n())
colusa_fd_tbl## # A tibble: 21 x 2
## year fd
## <dbl> <int>
## 1 2000 9
## 2 2001 14
## 3 2002 16
## 4 2003 10
## 5 2004 9
## 6 2005 5
## 7 2006 11
## 8 2007 23
## 9 2008 8
## 10 2009 24
## # ... with 11 more rows
5.6 Last Spring and First Fall Freeze
The Last Spring Freeze (LSF) is defined as the last day of the calendar year prior to 30 June with a Tn ≤ 0 °C. Conversely the First Fall Freeze (FFF) is defined as the first day of the calendar year commencing 1 July with Tn ≤ 0 °C (Parker et al. 2022).
We can find the last freeze date by chaining together dplyr expressions that i) keep only ‘freeze days’ from January through June, ii) group the freeze days by year, and iii) taking the max date for each group:
colusa_lf_tbl <- colusa_tbl %>%
filter(cvar == "tmmn", month(dt) <= 6, temp_f <= set_units(32, degF)) %>%
group_by(year) %>%
summarise(lf = max(dt))
colusa_lf_tbl## # A tibble: 20 x 2
## year lf
## <dbl> <date>
## 1 2000 2000-01-28
## 2 2001 2001-04-10
## 3 2002 2002-03-18
## 4 2003 2003-02-08
## 5 2004 2004-01-05
## 6 2005 2005-01-30
## 7 2006 2006-02-20
## 8 2007 2007-03-01
## 9 2008 2008-04-20
## 10 2009 2009-03-23
## 11 2011 2011-02-28
## 12 2012 2012-03-23
## 13 2013 2013-02-26
## 14 2014 2014-02-04
## 15 2015 2015-01-03
## 16 2016 2016-01-01
## 17 2017 2017-02-28
## 18 2018 2018-03-05
## 19 2019 2019-01-04
## 20 2020 2020-01-04
Similarly, we can find the first fall freeze by keeping only dates from July - December where the temperature dipped below freezing, then taking the minimum date for each year:
colusa_fff_tbl <- colusa_tbl %>%
filter(cvar == "tmmn", month(dt) >= 7, temp_f <= set_units(32, degF)) %>%
group_by(year) %>%
summarise(fff = min(dt))
colusa_fff_tbl## # A tibble: 20 x 2
## year fff
## <dbl> <date>
## 1 2000 2000-11-12
## 2 2001 2001-11-27
## 3 2002 2002-12-23
## 4 2003 2003-11-22
## 5 2004 2004-11-29
## 6 2005 2005-12-04
## 7 2006 2006-11-28
## 8 2007 2007-12-01
## 9 2008 2008-12-10
## 10 2009 2009-11-13
## 11 2010 2010-11-23
## 12 2011 2011-12-04
## 13 2012 2012-12-15
## 14 2013 2013-11-24
## 15 2015 2015-11-25
## 16 2016 2016-12-06
## 17 2017 2017-12-11
## 18 2018 2018-11-14
## 19 2019 2019-11-24
## 20 2020 2020-11-10
5.7 Freeze-Free Season
The Freeze-Free Season (FFS) is calculated as the difference between the LSF and FFF (FFF [minus] LSF) (Parker et al. 2022). Since we already calculated LSF and FFF, computing the Freeze-Free Season can be done with a simple table join:
colusa_lf_fff_tbl <- colusa_lf_tbl %>% left_join(colusa_fff_tbl, by = "year")
colusa_lf_fff_tbl %>% head()## # A tibble: 6 x 3
## year lf fff
## <dbl> <date> <date>
## 1 2000 2000-01-28 2000-11-12
## 2 2001 2001-04-10 2001-11-27
## 3 2002 2002-03-18 2002-12-23
## 4 2003 2003-02-08 2003-11-22
## 5 2004 2004-01-05 2004-11-29
## 6 2005 2005-01-30 2005-12-04colusa_lf_fff_ffs_tbl <- colusa_lf_fff_tbl %>% mutate(ffs = fff - lf)
colusa_lf_fff_ffs_tbl## # A tibble: 20 x 4
## year lf fff ffs
## <dbl> <date> <date> <drtn>
## 1 2000 2000-01-28 2000-11-12 289 days
## 2 2001 2001-04-10 2001-11-27 231 days
## 3 2002 2002-03-18 2002-12-23 280 days
## 4 2003 2003-02-08 2003-11-22 287 days
## 5 2004 2004-01-05 2004-11-29 329 days
## 6 2005 2005-01-30 2005-12-04 308 days
## 7 2006 2006-02-20 2006-11-28 281 days
## 8 2007 2007-03-01 2007-12-01 275 days
## 9 2008 2008-04-20 2008-12-10 234 days
## 10 2009 2009-03-23 2009-11-13 235 days
## 11 2011 2011-02-28 2011-12-04 279 days
## 12 2012 2012-03-23 2012-12-15 267 days
## 13 2013 2013-02-26 2013-11-24 271 days
## 14 2014 2014-02-04 NA NA days
## 15 2015 2015-01-03 2015-11-25 326 days
## 16 2016 2016-01-01 2016-12-06 340 days
## 17 2017 2017-02-28 2017-12-11 286 days
## 18 2018 2018-03-05 2018-11-14 254 days
## 19 2019 2019-01-04 2019-11-24 324 days
## 20 2020 2020-01-04 2020-11-10 311 days
5.8 Tropical Nights and Hot Days
Tropical Nights (TRN) are calculated as the number of nights per year with Tn > 20 °C (68 °F) (Parker et al. 2022). This can be computed with:
colusa_tn_tbl <- colusa_tbl %>%
filter(cvar == "tmmn", temp_f > set_units(20, degC)) %>%
group_by(year) %>%
summarise(tn = n())
colusa_tn_tbl## # A tibble: 18 x 2
## year tn
## <dbl> <int>
## 1 2000 10
## 2 2001 8
## 3 2002 3
## 4 2003 10
## 5 2004 1
## 6 2005 4
## 7 2006 12
## 8 2007 6
## 9 2008 6
## 10 2009 3
## 11 2011 2
## 12 2012 3
## 13 2013 13
## 14 2015 10
## 15 2017 15
## 16 2018 2
## 17 2019 3
## 18 2020 13
Hot Days (HD) are defined as when Tx > 38 °C (Parker et al. 2022). The number of hot days per year can be computed with:
colusa_hd_tbl <- colusa_tbl %>%
filter(cvar == "tmmx", temp_f > set_units(38, degC)) %>%
group_by(year) %>%
summarise(hd = n())
colusa_hd_tbl## # A tibble: 21 x 2
## year hd
## <dbl> <int>
## 1 2000 15
## 2 2001 17
## 3 2002 15
## 4 2003 14
## 5 2004 7
## 6 2005 20
## 7 2006 20
## 8 2007 8
## 9 2008 21
## 10 2009 26
## # ... with 11 more rows
5.9 Extreme Heat Days
Extreme Heat Days (EHD) are the number of days per year with Tx >98th percentile of summer (June-August) Tx for the 1981–2010 period (Parker et al. 2022). This is similar to HD, but with a threshold value based on the historic record. We can compute the 98th percentile of daily summertime highs with:
colusa_ehd_thresh <- ca_loc_pt(coords = c(-122.159304, 39.289291)) %>%
ca_slug("tmmx_day_gridmet") %>%
ca_years(start = 1981, end = 2010) %>%
ca_getvals_tbl(quiet = TRUE) %>%
filter(month(as.Date(dt)) %in% c(6,7,8)) %>%
pull(val) %>%
quantile(0.98) %>%
set_units(degF)
colusa_ehd_thresh## 106.2176 [degF]
Once we have that threshold, we can compute Extreme Heat Days with:
colusa_ehd_tbl <- colusa_tbl %>%
filter(cvar == "tmmx", temp_f > colusa_ehd_thresh) %>%
group_by(year) %>%
summarise(hd = n())
colusa_ehd_tbl## # A tibble: 17 x 2
## year hd
## <dbl> <int>
## 1 2001 1
## 2 2002 1
## 3 2003 4
## 4 2005 2
## 5 2006 7
## 6 2007 1
## 7 2008 4
## 8 2009 3
## 9 2010 1
## 10 2012 10
## 11 2013 12
## 12 2014 2
## 13 2015 1
## 14 2017 8
## 15 2018 1
## 16 2019 1
## 17 2020 3
5.10 Heatwaves
Heatwave events (HW) are defined as 3+ consecutive days with Tx > 98th percentile of 1981–2010 summer Tx (as in EHD) (Parker et al. 2022). Using the technique described in Chapter 4 - Counting Consecutive Events, we can compute the number of heatwaves per year.
- Add a column for extreme heat day, then create a grouped tibble (by year):
colusa_grpd_tbl <- colusa_tbl %>%
filter(cvar == "tmmx") %>%
mutate(ehd = temp_f > colusa_ehd_thresh) %>%
group_by(year) %>%
arrange(dt)
glimpse(colusa_grpd_tbl)## Rows: 7,671
## Columns: 5
## Groups: year [21]
## $ year <dbl> 2000, 2000, 2000, 2000, 2000, 2000, 2000, 2000, 2000, 2000, 200~
## $ dt <date> 2000-01-01, 2000-01-02, 2000-01-03, 2000-01-04, 2000-01-05, 20~
## $ cvar <chr> "tmmx", "tmmx", "tmmx", "tmmx", "tmmx", "tmmx", "tmmx", "tmmx",~
## $ temp_f [degF] 54.95 [degF], 53.87 [degF], 57.65 [degF], 49.37 [degF], 57.47 ~
## $ ehd <lgl> FALSE, FALSE, FALSE, FALSE, FALSE, FALSE, FALSE, FALSE, FALSE, ~
- Create a function that we can pass to
group_modify(), will return the number of heatwaves per group (year):
num_hw <- function(data_tbl, key_tbl, num_days = 3) {
rle_lst <- rle(data_tbl$ehd)
tibble(num_hw = sum(rle_lst$values & rle_lst$lengths >= num_days))
}
- Apply the heatwave function to the grouped tibble:
colusa_hw_tbl <- colusa_grpd_tbl %>%
group_modify(.f = num_hw, num_days = 3)
colusa_hw_tbl## # A tibble: 21 x 2
## # Groups: year [21]
## year num_hw
## <dbl> <int>
## 1 2000 0
## 2 2001 0
## 3 2002 0
## 4 2003 0
## 5 2004 0
## 6 2005 0
## 7 2006 1
## 8 2007 0
## 9 2008 1
## 10 2009 0
## # ... with 11 more rows
5.11 Diurnal Temperature Range
Diurnal Temperature Range (DTR) is the difference between daily Tx and Tn (Parker et al. 2022). Below we calculate DTR over 1 March to 1 November.
colusa_dtr_tbl <- colusa_tbl %>%
filter(month(dt) %in% 3:10) %>%
pivot_wider(id_cols = c(year, dt), names_from = cvar, values_from = temp_f) %>%
mutate(dtr = tmmx - tmmn)
head(colusa_dtr_tbl)## # A tibble: 6 x 5
## year dt tmmn tmmx dtr
## <dbl> <date> [degF] [degF] [degF]
## 1 2000 2000-03-01 35.7 62.7 27.0
## 2 2000 2000-03-02 45.9 55.5 9.54
## 3 2000 2000-03-03 36.6 68.6 32.0
## 4 2000 2000-03-04 41.1 62.1 21.1
## 5 2000 2000-03-05 46.3 55.5 9.18
## 6 2000 2000-03-06 43.6 56.4 12.8ggplot(colusa_dtr_tbl %>% mutate(year = as.factor(year)), aes(x=year, y = dtr)) +
geom_boxplot() +
labs(title = "Diurnal Temperature Range, 2000-2020",
subtitle = "Colusa, CA",
caption = "Dataset: gridMet. Temporal period: March - October",
x = "", y = "daily temperature range")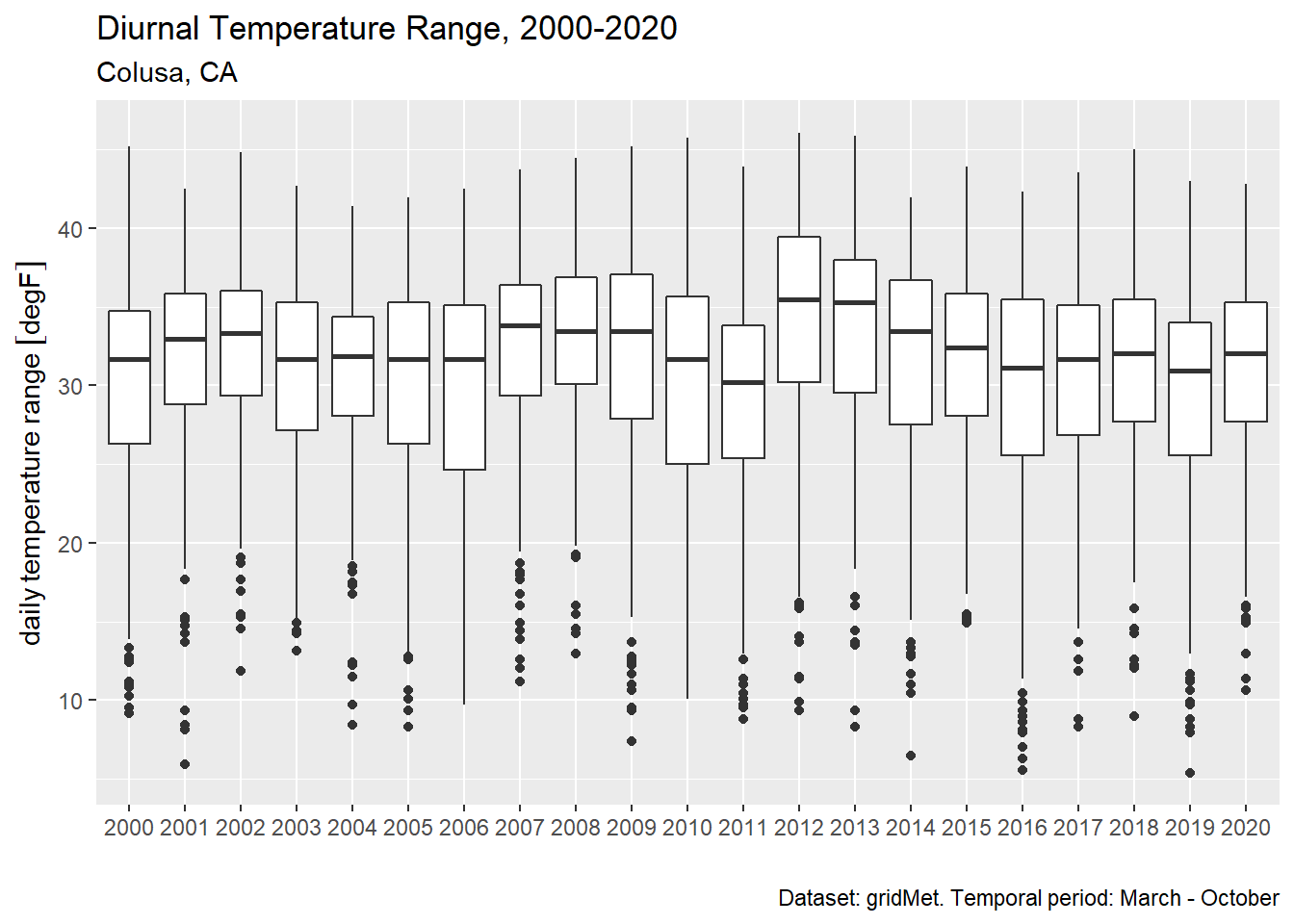
5.12 Reference Evapotranspiration
ETo is calculated following the FAO Penman–Monteith method (Allen and United Nations 1998). We calculate summer (June-August) average ETo for each year 1981–2020 for our analysis. ETo units are mm (Parker et al. 2022).
More coming soon…